Autodesk Inventor. Functii mai mult sau mai putin cunoscute
Episodul 2. Curbe prin ecuatii (Equation Curve)
Curbele generate din ecuatii sunt folosite pentru a modela geometrii complexe, de exemplu profilurile danturii angrenajelor sau corpul spiralat al unei pompe centrifugale. Pentru a genera o curba dintr-o ecuatie se specifica ecuatiile care definesc curba si un interval de valori ale acestora.
Ecuatiile pot fi parametrice, caz in care X si Y variaza ca functie de variabila t sau explicite, unde Y variaza direct functie de X.
De exemplu, pentru a modela o parabola se utilizeaza una din variantele:
1. Parametric: x(t) = t si y(t) = t^2, sau
2. Explicit: y(x) = x^2 / 1 mm
Curbele 2D din ecuatii accepta atat sistemele de coordonate carteziene cat si polare.
Curbele cu coordonate polare necesita coordonatele ca vector (r) si unghi (θ).
Curbele cu coordonate carteziene utilizeaza coordonatele X, Y.
De asemenea, curbele din ecuatii accepta parametri si functii.
Exceptia pentru parametri este ca nu puteti avea un parametru numit „t” – deoarece acesta este deja folosit de aplicatie pentru variabila din ecuatii.
In exemplul descris mai jos, vom crea o spirala cu pas variabil folosind aceasta functionalitate, Equation Curve.
Pe scurt, se creaza o schita noua 3D Sketch si se lanseaza comanda Equation Curve.
Variante posibile:
Prin coordonate carteziene:
x(t) = raza * sin(360 * numar_spire * t)
y(t) = raza * cos(360 * numar_spire * t)
z(t) = inaltime * t (sau) = numar_spire * pasul * t
Prin coordonate polare:
r(t) = raza
theta(t) = 360 * numar_spire * t
z(t) = inaltime * t (sau) = numar_spire * pasul * t
Pentru a varia raza, se inlocuieste raza cu raza * t.
Pentru a varia pasul, se inlocuieste pasul cu pasul * t.
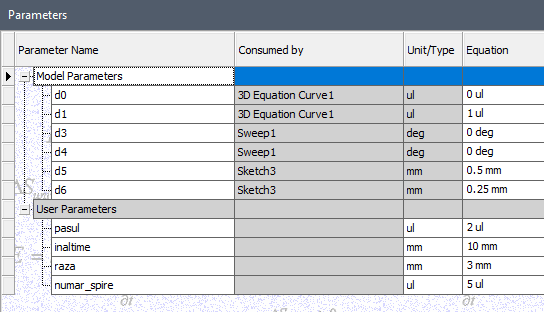
Exemplu practic de valori:
raza = 3 sau 3*t
numar_spire = 5
inaltime = 10
pasul = 2 sau 2*t
cu “t” in intervalul de valori (0 – 1).
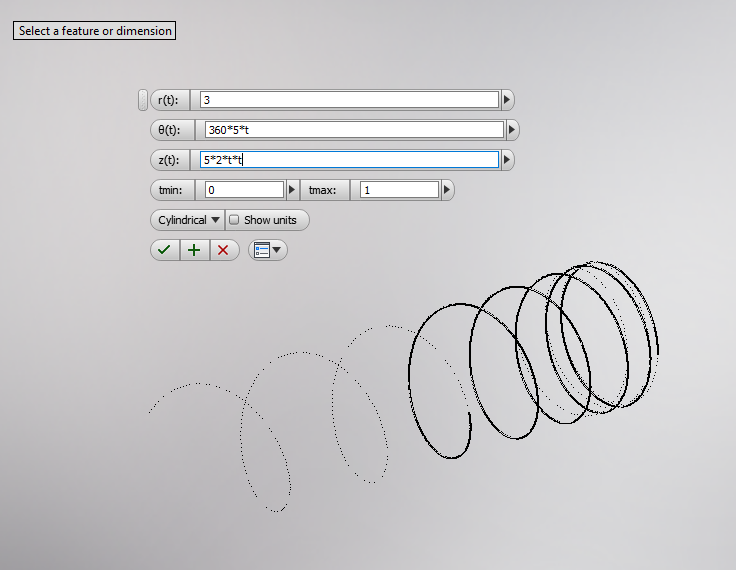
1. raza constanta, pasul variabil:
Prin coordonate carteziene:
x(t) = 3*sin(360*5*t)
y(t) = 3*cos(360*5*t)
z(t) = 5*2*t*t

Prin coordonate polare:
r(t) = 3
theta(t) = 360*5*t
z(t) = 5*2*t*t
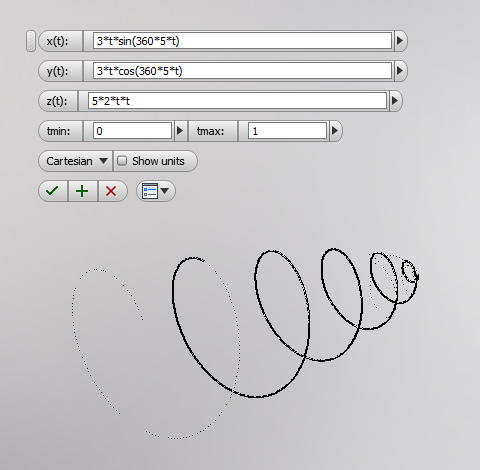
2. raza variabila, pasul variabil:
Prin coordonate carteziene:
x(t) = 3*t*sin(360*5*t)
y(t) = 3*t*cos(360*5*t)
z(t) = 5*2*t*t
Prin coordonate polare:
r(t) = 3*t
theta(t) = 360*5*t
z(t) = 5*2*t*t
Sintaxa t*t poate fi inlocuita cu t^2.
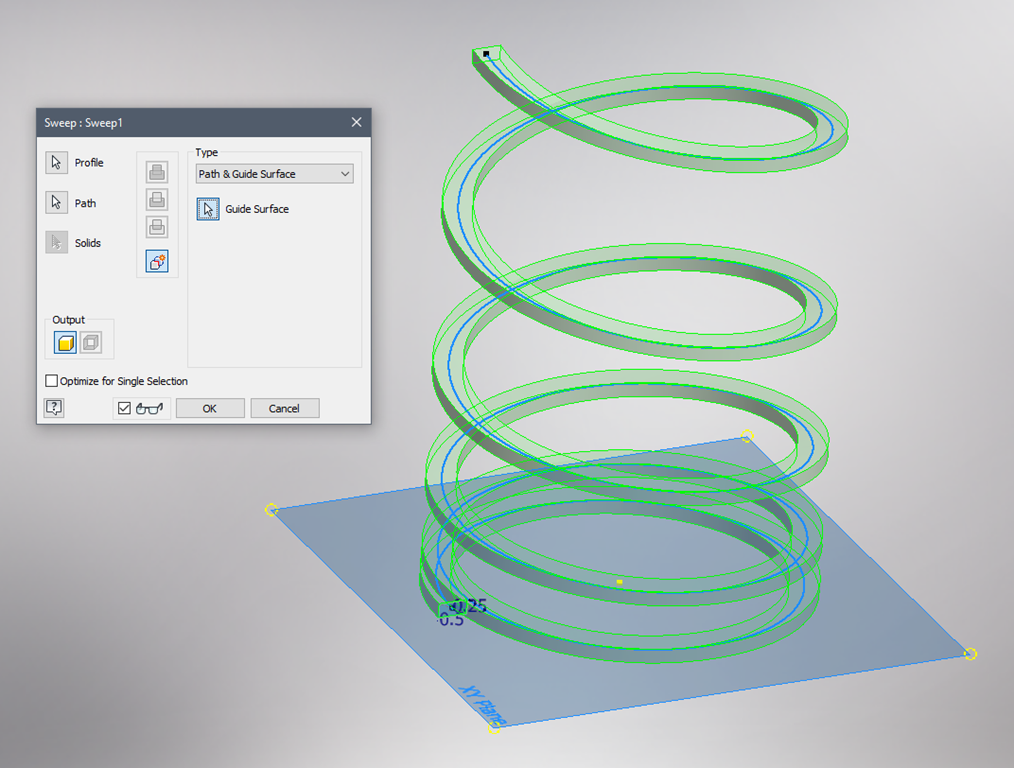
Nota: atunci cand se utilizeaza functia Sweep, se va utiliza optiunea Path & Guide Surface care sa orienteze sectiunea dupa curba (spirala), folosind ca referinta planul XY, in acest caz.
Citeste si episodul 1. – Sketch Driven Pattern